HYDROSTATIQUE
Définition
C'est la branche de la science hydraulique qui étudie l'équilibre des fluides
Rappels
MASSE VOLUMIQUE
C'est la masse par unité de volume
\[ \rho = kg \times m^{-3} \]
\[ \rho_{eau} = 1000 \space kg \space m^{-3} \]
DENSITE
C'est le rapport entre la masse volumique du fluide étudié et la référence, l'eau
\[ d_{fluide} = \frac{\rho_{fluide}}{\rho_{eau}}\]
\[d_{eau} = 1 \]
PRESSION
C'est le rapport entre le poids et la surface, exprimé en Pascal (Pa)
\[ P = \frac{\vec{P}}{S} = \frac{ m \space \vec{g}}{S}\]
\[10^5 \space Pa = 1 \space Bar \]
\[1 \space Bar = 10,2 \space mCE \]
Bar provient du grec ancien βάρος / báros qui signifie lourd et mCE pour mètres de Colonne d'Eau
Pression relative / Pression absolue
Energies
POTENTIELLE DE PESANTEUR
\[ Epp = m \times g \times z \]
z pour l'altitude en m
\[kg \space m \space s^{-2} = N \]
En hydraulique
\[ Epp = \rho \times g \times z \] \[kg \space m^{-1} \space s^{-2} = Pa \]
PRESSION
\[ Epr = \frac{m \times g}{S} \] \[kg \space m^{-1} \space s^{-2} = Pa \]
CINETIQUE
\[ Ec = \frac{1}{2} \times m \times v^2 \] \[kg \space m \space s^{-2} = N \]
En hydraulique
\[ Ec = \frac{1}{2} \times \rho \times v^2 \] \[kg \space m^{-1} \space s^{-2} = Pa \]
TOTALE
\[ Et = Epp + Epr + Ec\]
Théorème de Bernouilli
FONDEMENTS
Le long d'une ligne de courant l'énergie du système se conserve
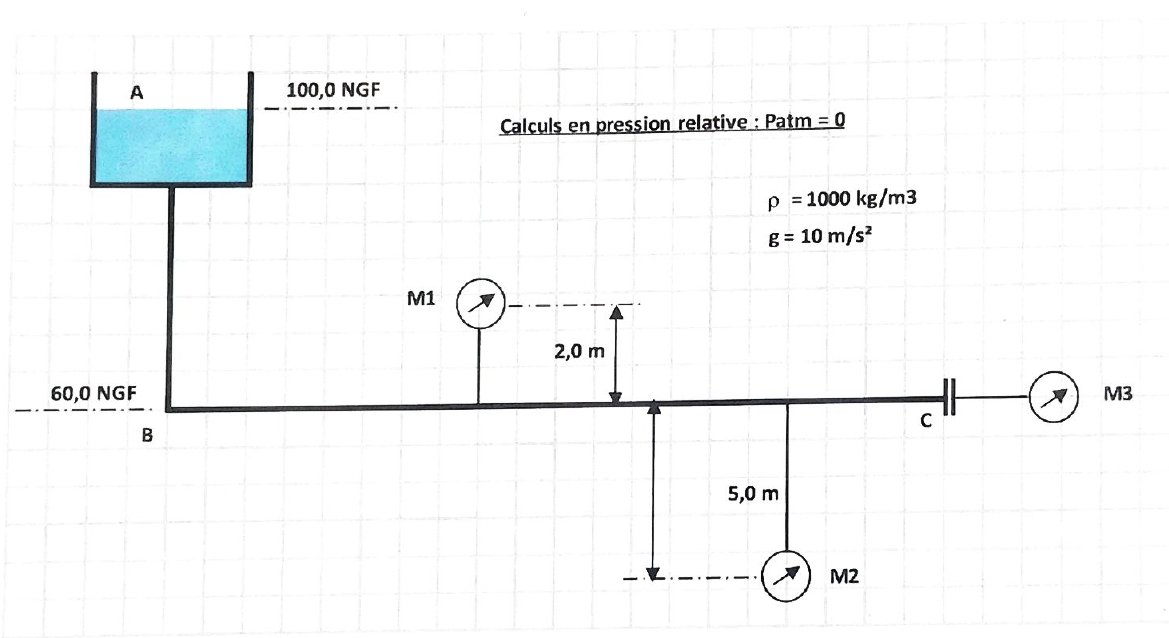
Voici le bilan énergétique entre deux points, A et B
Démonstration
FORMULE
\[ z_A + \frac{P_A}{\rho g} + \frac{v_A^2}{2g} \]\[= \]\[z_B + \frac{P_B}{\rho g} + \frac{v_B^2}{2g} \]
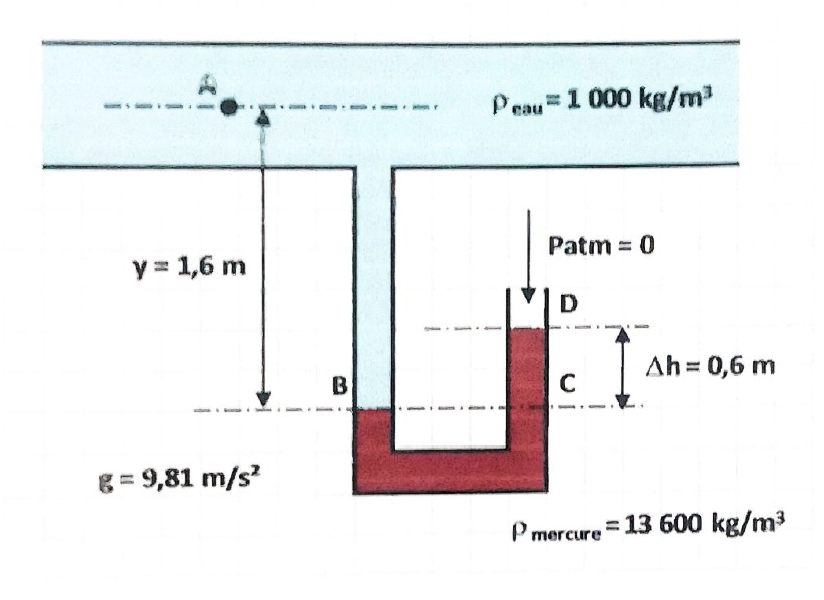
EN HYDROSTATIQUE
En hydrostatique les fluides n'ont pas de débit donc pas de vitesse d'écoulement
\[ z_A + \frac{P_A}{\rho g}= z_B + \frac{P_B}{\rho g}\]
\[ \frac{P_A}{\rho g} - \frac{P_B}{\rho g} = z_B - z_A \]
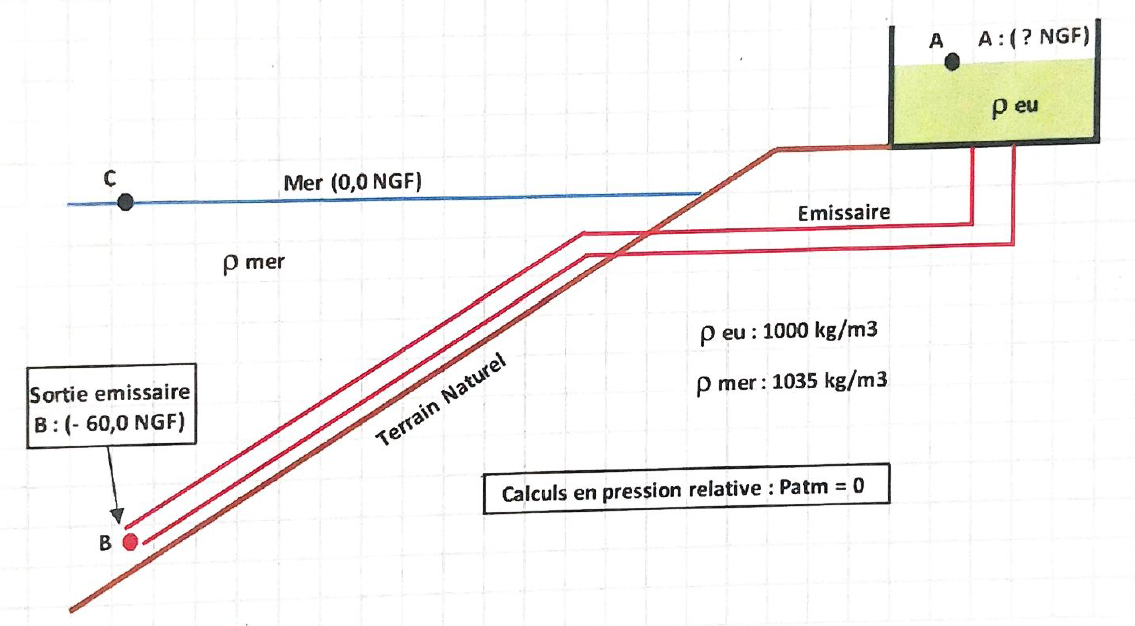
\[ P_A - P_B = \rho g (z_B - z_A) \]
La formule ci-dessus est la relation fondamentale de l'hydrostatique (RFH)
REMARQUE
Pour pouvoir appliquer cette formule, 3 conditions doivent être respectées
Le fluide doit être incompressible
Le fluide doit être parfait
Le régime d'écoulement doit être constant
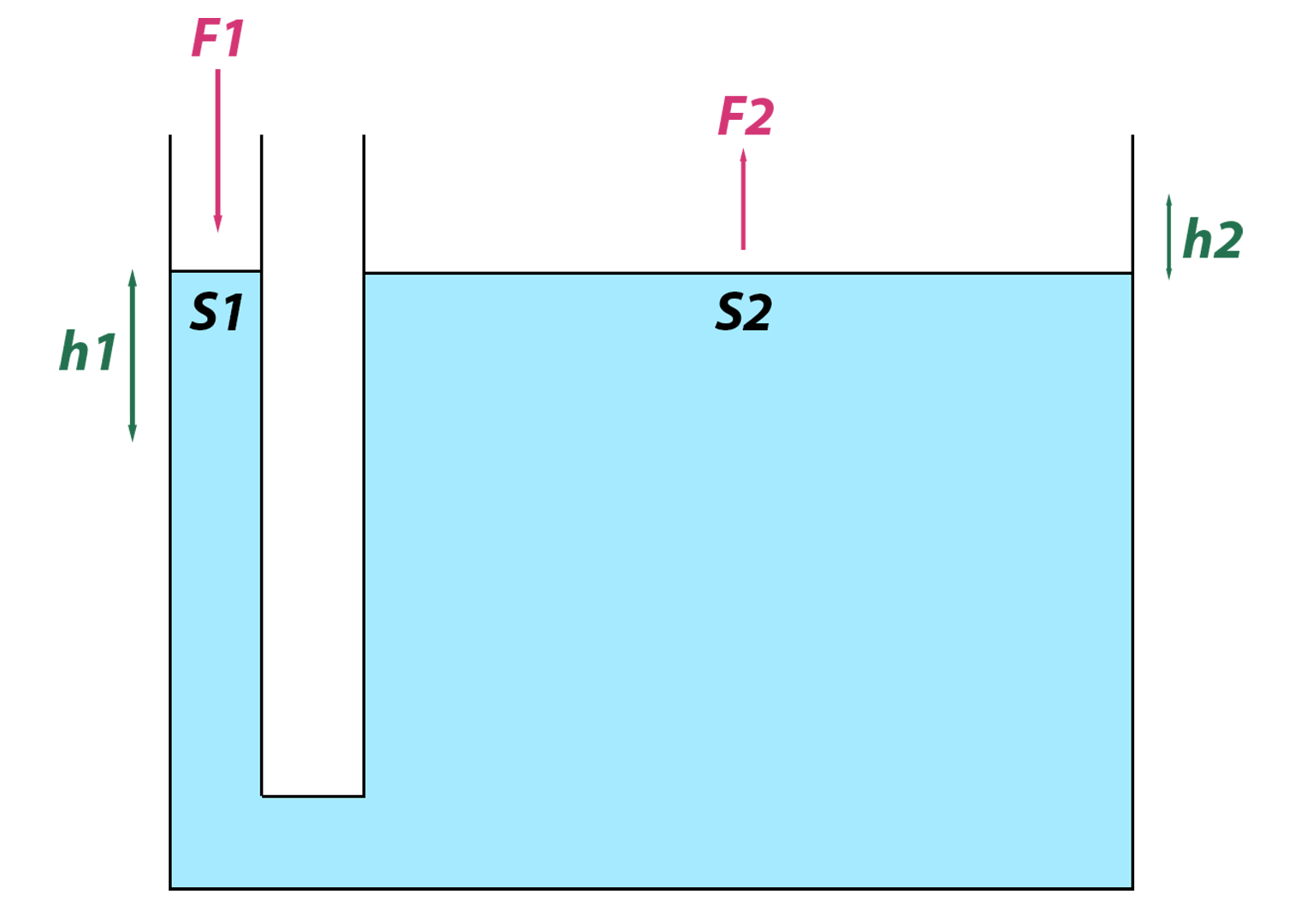
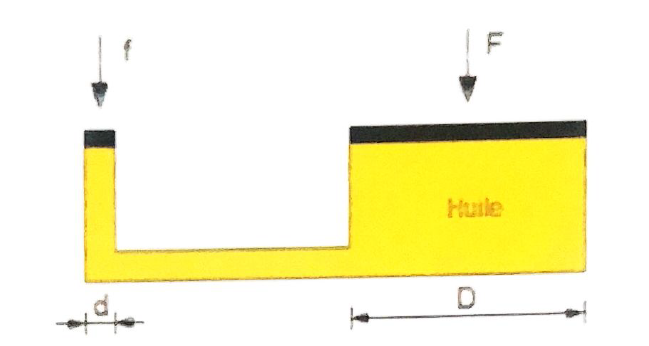
Principes de Pascal
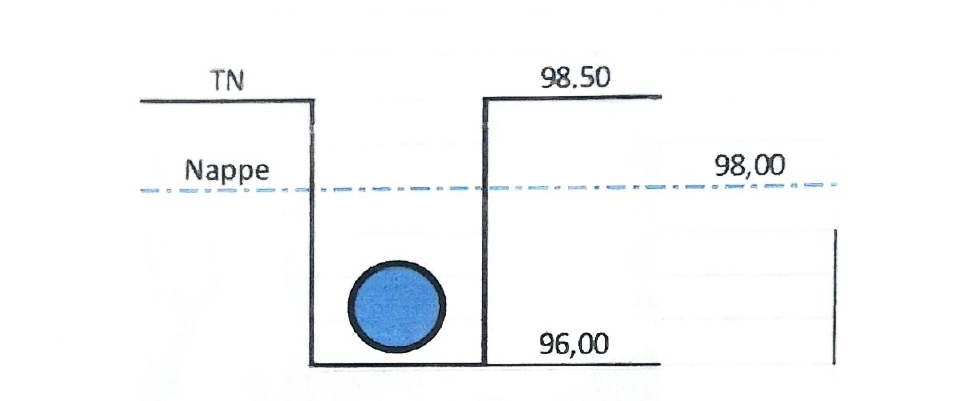
Dans un liquide en équilibre de masse volumique uniforme, la pression est la même en tout point de la même profondeur
S'il y a une variation de pression en un point
Il y aura une variation de la même valeur pour tous les autres
\[ \frac{F1}{S1} = \frac{F2}{S2} \] \[ F1 \times h1 = F2 \times h2 \]
Archimède
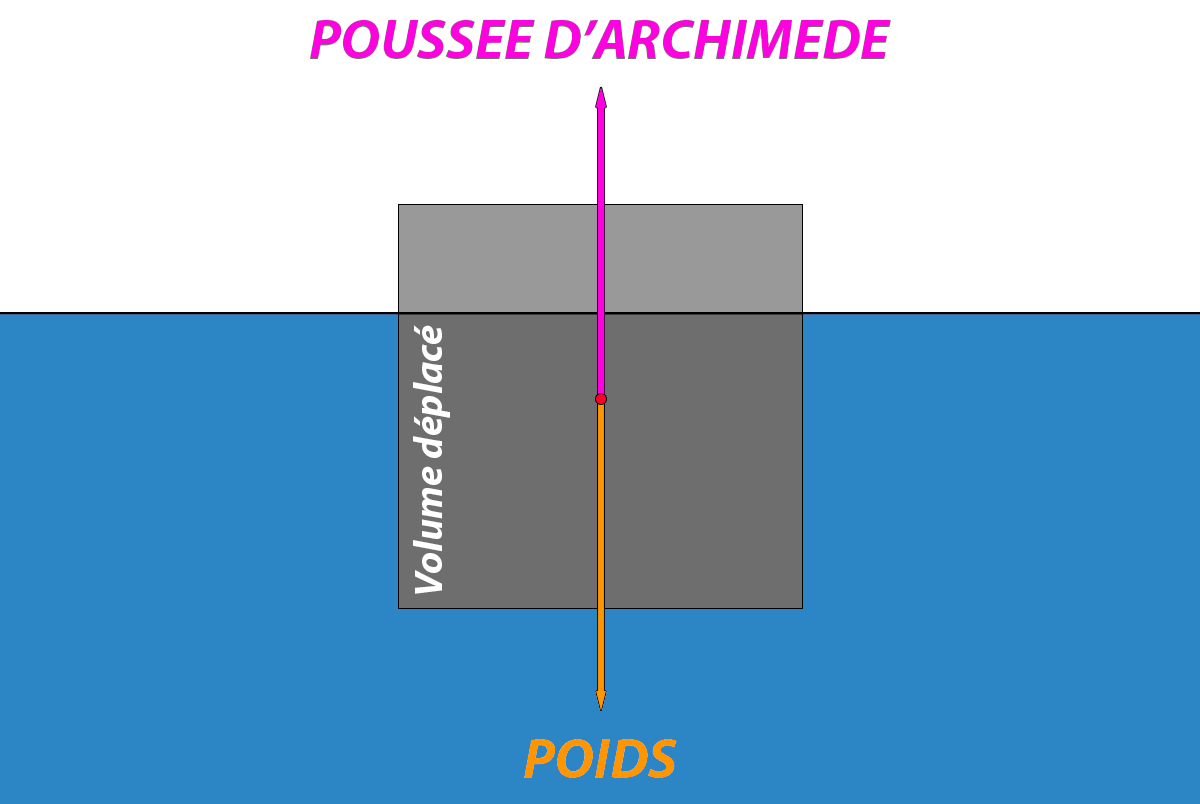
DEFINITION
Tout corps plongé dans un liquide reçoit de celui-ci une force (ou poussée verticale) dirigée vers le haut dont l'intensité est égale au poids du volume de liquide déplacé
FORMULE
\[P_{archimede}\]\[ =\] \[V_{deplace}\times \rho_{liquide}\times g\]
PRECISIONS
Lorsqu'un objet est dans un liquide, de manière générale, il est soumis à deux forces
La poussée d'Archimède vers le haut
Son poids vers le bas
Si le poids est plus important que la poussée, l'objet coule (sinon l'objet flotte)
Si ces deux forces sont égales, l'objet se maintien
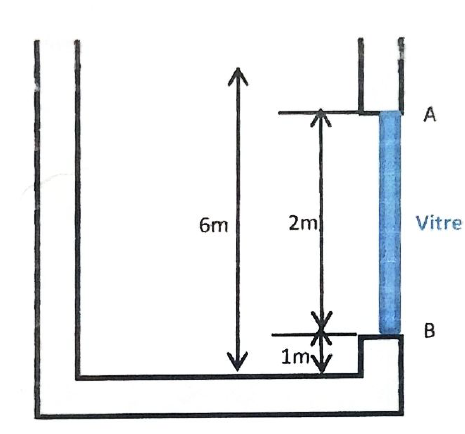
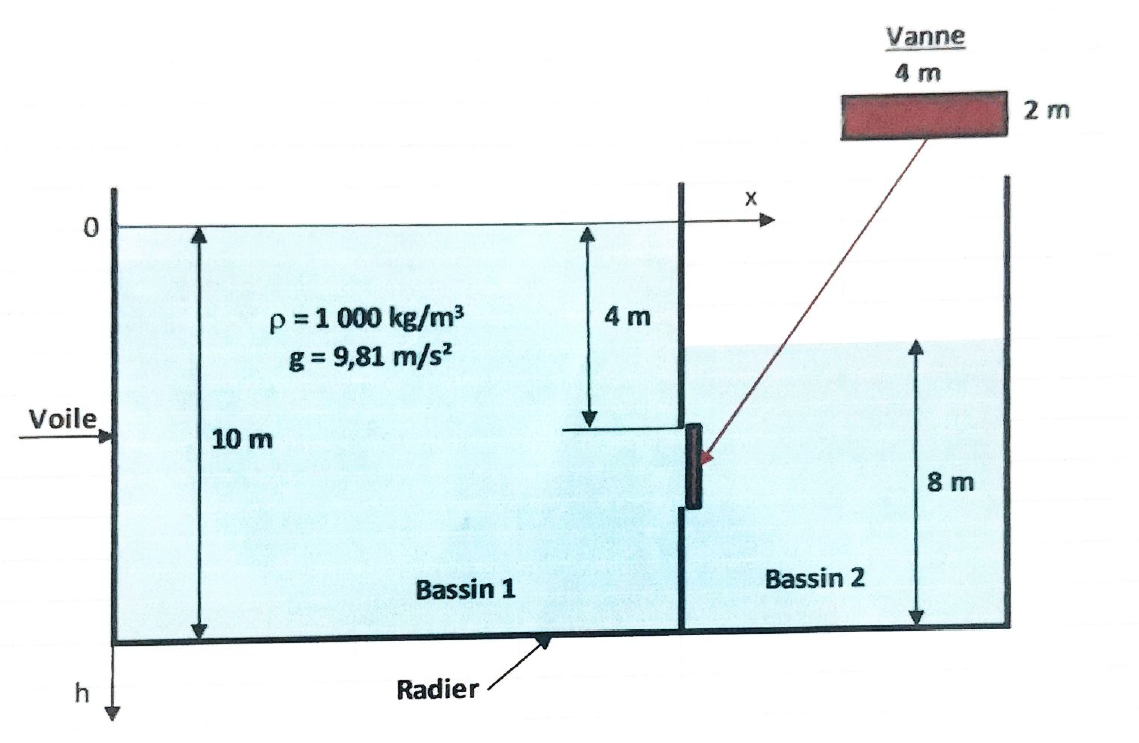
Poussée hydrostatique
C'est la pression exercée par un fluide sur une surface
\[ F_{poussee} = \rho \times g \times h_{gravite} \times S \]
\( h_{gravite} \) est la hauteur d'eau entre la surface et le centre de gravité de l'objet
La représentation de cette force (par un vecteur) est appliquée en un point précis
\[ z_{application}\]\[ = \] \[h_{gravite} + \frac{I}{h_{gravite}\times S} \]
I correspond au moment quadratique
\[ I_{rectangle} = \frac{bh^3}{12} \]
\[ I_{cercle} = \frac{\pi r^4}{64} \]
Exercices
Supports
VIDEOS
RFH et Torricelli
Statique des fluides
(partie 1)
Statique des fluides
(partie 2)
Statique des fluides
(partie 3)
DOCUMENTS
Cours d'hydrostatiques et exercices d'application
Cours d'hydrostatiques et exercices d'application 2
LIENS
